Legendary Dutch computer scientist Edsger W Dijkstra famously remarked that “testing shows the presence, not the absence of bugs”. In fact the only definitive way to establish that software is correct and bug-free is through mathematics.
It has long been known that software is hard to get right. Since Friedrich L Bauer organized the very first conference on “software engineering” in 1968, computer scientists have devised methodologies to structure and guide software development. One of these, sometimes called strong software engineering or more usually formal methods, uses mathematics to ensure error-free programming.
As the economy becomes ever more computerized and entwined with the internet, flaws and bugs in software increasingly lead to economic costs from fraud and loss. But despite having heard expert evidence that echoed Dijkstra’s words and emphasizes the need for the correct, verified software that formal methods can achieve, the UK government seems not to have got the message.
Read Also: Building privacy right into software code
Formal software engineering
The UK has always been big in formal methods. Two British computer scientists, Tony Hoare (Oxford 1977-, Microsoft Research 1999-) and the late Robin Milner (Edinburgh 1973-95, Cambridge 1995-2001) were given Turing Awards – the computing equivalent of the Nobel Prize – for their work in formal methods.
British computer scientist Cliff B Jones was one of the inventors of the Vienna Development Method while working for IBM in Vienna, and IBM UK and Oxford University Computing Laboratory, led by Tony Hoare, won a Queen’s Award for Technological Achievement for their work to formalise IBM’s CICS software. In the process they further developed the Z notation which has become one of the major formal methods.
The formal method process entails describing what the program is supposed to do using logical and mathematical notation, then using logical and mathematical proofs to verify that the program indeed does what it should. For example, the following Hoare logic formula describing a program’s function shows how formal methods reduce code to something as irreducibly true or false as 1 + 1 = 2.
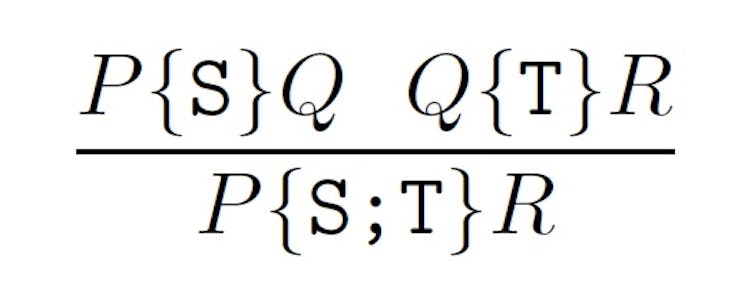
Taught at most UK universities since the mid-1980s, formal methods have seen considerable use by industry in safety-critical systems. Recent advances have reached a point where formal methods’ capacity to check and verify code can be applied at scale with powerful automated tools.
Government gets the message
Is there any impetus to see them used more widely, however? When the Home Affairs Committee took evidence in its E-crime enquiry in April 2013, Professor Jim Norton, former chair of the British Computer Society, told the committee:
We need better software, and we know how to write software very much better than we actually do in practice in most cases today… We do not use the formal mathematical methods that we have available, which we have had for 40 years, to produce better software.
Based on Norton’s evidence, the committee put forward in recommendation 32 “that software for key infrastructure be provably secure, by using mathematical approaches to writing code.”
Two months later in June, the Science and Technology Committee took evidence on the Digital by Default programme of internet-delivered public services. One invited expert was Dr Martyn Thomas, founder of Praxis, one of the most prominent companies using formal methods for safety-critical systems development. Asked how to achieve the required levels of security, he replied that:
Heroic amounts of testing won’t give you a high degree of confidence that things are correct or have the properties you expect… it has to be done by analysis. That means the software has to be written in such a way that it can be analyzed, and that is a big change to the way the industry currently works.
The committee sent an open letter to cabinet secretary Francis Maude in asking whether the government “was confident that software developed meets the highest engineering standards.”
Trustworthy software is the answer
The government, in its response to the E-crime report in October 2013 , stated:
The government supports Home Affairs Committee recommendation 32. To this end the government has invested in the Trustworthy Software Initiative, a public/private partnership initiative to develop guidance and information on secure and trustworthy software development.
This sounded very hopeful. Maude’s reply to the Science and Technology committee that month was not published until October 2014, but stated much the same thing.
So one might guess that the TSI had been set up specifically to address the committee’s recommendation, but this turns out not to be the case. The TSI was established in 2011, in response to governmental concerns over (cyber) security. Its “initiation phase” in which it drew from academic expertise on trustworthy software ended in August 2014 with the production of a guide entitled the Trustworthy Security Framework, available as British Standards Institute standard PAS 754:2014.
This is a very valuable collection of risk-based software engineering practices for designing trustworthy software (and not, incidentally, the “agile, iterative and user-centric” practices described in the Digital by Default service manual). But so far formal methods have been given no role in this. In a keynote address at the 2012 BCS Software Quality Metrics conference, TSI director Ian Bryant gave formal methods no more than a passing mention as a “technical approach to risk management”.
So the UK government has been twice advised to use mathematics and formal methods to ensure software correctness, but having twice indicated that the TSI is its vehicle for achieving this, nothing has happened. Testing times for software correctness, then, something that will continue for as long as it takes for Dijkstra’s message to sink in.
Eerke Boiten, Senior Lecturer, School of Computing and Director of Interdisciplinary Cyber Security Centre, University of Kent
This article is republished from The Conversation under a Creative Commons license. Read the original article.
Z notation was developed by Jean-Raymond Abrial. He first started working on what would later become Z in 1974.
Z was originally proposed by Abrial in 1977 with the help of Steve Schuman and Bertrand Meyer.
Abrial went to Oxford in September 1979.